od noox » 30. 5. 2011 13:49
skupina A:
1.) Zformulujte a dokazte vetu o charakterizaci positivne definitnich matic. (7)
Definujte ortogonalni matici. (1)
2.) Mejte matici radu n:
A = na diagonale 5ky jinak vsude 2ky
a.) Spocitejte det(A). (3)
b.) Spocitejte A
11-1. (3)
3.) Bud A =
2 2 1
2 5 2
1 2 2
Najdete spektralni rozklad matice A. (6) - vlastni cisla: 1,1,7; vektory: (-2,1,0), (-1,0,1), (1,2,1)
4.) Rozhodnete a zduvodnete, ktera z nasledujicich tvrzeni jsou pravdiva.
a.) Adjungovana matice k dolni trojuhelnikove matici je opet dolni trojuhelnikova matice. (2) - ano
b.) Existuji vektory u,v,w z R
2 delky jedna takove, ze <u,v>=<v,w>=<w,u>=0. (2) - ano
c.) Jsou-li matice A, B podobne, pak i A+I, B+I jsou podobne. (2) - ano
d.) Pro kazdou matici A plati
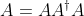
. (2) - ano
Na 4ku je oproti minulemu semestru potreba 7 bodu, na 3ku 12, (to dost lidi vydesilo:D)
na 2ku 18, na 1ku 24.skupina A:
1.) Zformulujte a dokazte vetu o charakterizaci positivne definitnich matic. (7)
Definujte ortogonalni matici. (1)
2.) Mejte matici radu n:
A = na diagonale 5ky jinak vsude 2ky
a.) Spocitejte det(A). (3)
b.) Spocitejte A[sub]11[/sub][sup]-1[/sup]. (3)
3.) Bud A =
2 2 1
2 5 2
1 2 2
Najdete spektralni rozklad matice A. (6) - vlastni cisla: 1,1,7; vektory: (-2,1,0), (-1,0,1), (1,2,1)
4.) Rozhodnete a zduvodnete, ktera z nasledujicich tvrzeni jsou pravdiva.
a.) Adjungovana matice k dolni trojuhelnikove matici je opet dolni trojuhelnikova matice. (2) - ano
b.) Existuji vektory u,v,w z R[sup]2[/sup] delky jedna takove, ze <u,v>=<v,w>=<w,u>=0. (2) - ano
c.) Jsou-li matice A, B podobne, pak i A+I, B+I jsou podobne. (2) - ano
d.) Pro kazdou matici A plati [latex]A=AA^\dagger A[/latex]. (2) - ano
[b]Na 4ku je oproti minulemu semestru potreba 7 bodu, na 3ku 12, [/b] (to dost lidi vydesilo:D) [b] na 2ku 18, na 1ku 24.[/b]